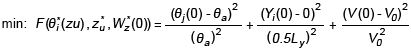QFN向け優れたPCBパッド設計を実現する要素

電子部品パッケージ技術が小型・軽量・高性能化へと発展するにつれて、電子部品の機能密度を高め、入力端子と出力端子間の間隔を縮小することが開発動向となっており、これは自動組立技術によって最もよく示されている。SMT（表面実装技術）. 部品の表面実装を行うためには、まず PCB 上に対応するパッドを作成して、所定の構造を持つ PCB を得る必要がある。その後、ステンシル印刷技術を用いて、PCB パッド表面にソルダーペーストを塗布する。最後に加熱を行い、ソルダーペーストを液体に変化させ、部品のピンと PCB パッドの間に液体ブリッジを形成させる。PCB 上のソルダーレジストの作用により、溶融したソルダーペーストは対応するソルダーパッド領域内に制限され、はんだ接合部同士のブリッジを防止することで、チップの PCB への自動実装が実現される。パッケージの種類に応じて、主に円形および長方形のソルダーパッドが選択される。すなわち、BGA（ボールグリッドアレイ）および QFN（クワッド・フラット・ノーリード）パッケージです。BGA についてもっと知りたい場合は、たった4つのステップで十分です。

QFNウィキ

他のさまざまなパッケージ形態の部品と比較して、QFNパッケージはPCBまたはFPC基板上に直接はんだ付けされるよう設計されています。底面に露出した金属パッドを有しているため、優れた放熱性能を発揮します。さらに、QFNパッケージは、リードが外形パッケージ部品よりも短いことから、優れた電気特性を備えています。したがって、PCB上にQFNパッドを適切に設計することは、PCBの高い信頼性と性能を維持・確保するうえで非常に重要です。

濡れ角

QFNピンのサイズおよびピン間の間隔が比較的小さいため、はんだペーストの塗布量が正確でないと、はんだブリッジや擬似はんだ付けが発生する可能性があります。したがって、ステンシルの厚さに基づいてPCBのパッドサイズを合理的に設計することにより（h₀) ははんだ付けの成功率に大いに役立つ。はんだパッド上のはんだ錫のぬれ角を仮定し (θ_a) は30°であり、ソルダーマスク上のはんだ付け錫の濡れ角（θ_rは 160°である。パッド表面の粗さを無視すると、濡れ角は三相接触線の前進角または後退角とほぼみなすことができる。QFN 部品の実際のはんだ付け工法に従い、はんだが十分に溶融しパッド表面が完全に濡れた理想状態の下でリフローはんだ付けの温度プロファイルを適切に制御することで、はんだ付け効率を確保するとともに、部品が自動的に実装はんだ付けのバランス状態に到達するのを助けることができる。パッドが適切に設計されていれば、はんだ接合部の理想的な状態は、PCB の電気的性能および機械的接続の要求を満たすだけでなく、ブリッジや擬似はんだ付けなどのはんだ接合不良を回避することができる。したがって、はんだ接合部の状態は次の式を満たさなければならない。

a. QFN内部のはんだ接合部がPCBパッド上に完全に分布している場合、θ_a≤θ_j(Z_u)≤θ_r,θ_j(0)=30°x₃(0)=x₄(0)=D_x4

b. QFN 外側の錫がサイドパッド上に成長している場合、

(1)θ_j(Z_u)=θ_s3+90°θ₄(0)=30°θ₃(0)=30°

(2)x₃(0)=x₄(0)=D_x4(0)、x₃(Z_u)=0.

パッド設計

この式では、θ_s3に等しいθ_aどちらも、側面パッド上のはんだスズの濡れ角である。

鉛直方向において、架橋液体の静力学的平衡方程式は次のようになる。
P_dL_y(x₃(0)-x₄(0)+L_x)+W_ｚ-[T(x₃(0)-x₄(0)+L_x)(サインθ₂(0)+サインθ₁(0))+TL_y(サインθ₃(0)+サインθ₄(0))]-ρgV₀=0

はんだ接合部の底部における圧力強度（P_d) は次のとおりです:P_d=【T(x₃(0)-x₄(0)+L_x)(サインθ₂(0)+サインθ₁(0))+TL_y(サインθ₃(0)+サインθ₄(0))+ρgV₀-W_z]/[L_y(x₃(0)-x₄(0)+L_x)]

これらの式では、ρはんだの液体密度を指し、T ははんだ接合部液体の表面張力を指す。x₃(0) とx₄(0) は、底部のはんだパッド上の液状はんだ接合部の両端におけるずれを指す。θ₁(0) とθ₂(0) は、はんだ接合部の両側において、液体‐気体界面が形成する両側の接触角と、底部パッド表面との間で形成される接触角を指すθ₃(0) とθ₄(0) は、両側の液体-気体界面によって両端に形成される接触角を指す。V₀はんだ接合部の体積を指します。W_ｚチップ端部およびはんだ接合部において、垂直方向に加えられるパッドの作用力を指す。

式（1）および（2）の制限の下で、はんだ接合部のフレーム曲線は、初期値問題の有効な解法に基づき、はんだ接合部上端の境界条件を初期条件と等価にすることができる。初期値問題の解は、次の要件を満たすことができないため、z0 に等しい場合、目的関数の最小化という観点から同等の問題に変換され、その内容は式 (3) に示される。

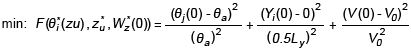
この最小化された目的関数は、パッドの理想的な設計サイズを決定するために適用することができるD_x4。

さらに、PCB パッドのはんだ巻き付き角の幾何学的特性も考慮に入れる必要があります。その観点から、パッドの拡張サイズは、以下のおおよその式に従うべきです。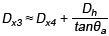

この方程式では、D_hチップ外側に露出しているサイドパッドの厚さを指す。暗黙変数の最適化を通じて、目的関数によって期待される誤差要件が満たされ、内側および外側のパッドの設計サイズが（D_x4&D_x3) は、下端での辺の値の必要性が満たされている場合に計算することができます。

この方法により、QFN に適したパッドを適切に設計して、この部品と PCB の双方において高い電気的性能を実現することができます。その後、専門的で資格を有する組立能力PCBCart は、お客様の理想的な設計を現実のものにすることができます。

役立つリソース
•ビアインパッド（VIP）技術の紹介
•SMT基板の設計要件 第1部：一般的な部品のランド設計
•SMT基板の設計要件 パート2：パッドと配線の接続、スルーホール、テストポイント、ソルダーレジストおよびシルク印刷の設定
•PCBA の最適な性能を実現するための QFN コンポーネントにおけるステンシル設計要件
•PCBCart のフル機能 PCB 製造サービス - 複数の付加価値オプション
•PCBCart の高度な PCB アセンブリサービス - 1 個から対応