ด้วยความซับซ้อนที่เพิ่มขึ้นของการออกแบบ PCB การจ่ายพลังงานที่เสถียรและเชื่อถือได้ได้กลายเป็นแนวโน้มใหม่ของการวิจัยเกี่ยวกับการออกแบบแผงวงจรพิมพ์ความเร็วสูงโดยเฉพาะอย่างยิ่งเมื่อจำนวนขององค์ประกอบสวิตชิ่งเพิ่มขึ้นอย่างต่อเนื่องและค่า Vcore ลดลงอย่างต่อเนื่อง ความผันผวนของพลังงานมีแนวโน้มที่จะก่อให้เกิดผลกระทบร้ายแรงต่อระบบ ดังนั้น การรักษาเสถียรภาพของระบบจ่ายไฟจึงกลายเป็นจุดสำคัญในการออกแบบ PCB ความเร็วสูง
อย่างไรก็ตาม เนื่องจากการมีอยู่ของอิมพีแดนซ์ในระบบไฟฟ้า ทำให้เกิดแรงดันตกค่อนข้างมากจากกระแสทรานเชียนต์ของโหลดในอิมพีแดนซ์ของระบบไฟฟ้า ซึ่งนำไปสู่ความไม่เสถียรของระบบ เพื่อให้มั่นใจว่าสามารถจ่ายพลังงานได้ตามปกติให้กับแต่ละองค์ประกอบตั้งแต่ต้นจนจบ จำเป็นต้องควบคุมอิมพีแดนซ์ในระบบไฟฟ้า ซึ่งหมายความว่าอิมพีแดนซ์ควรถูกลดให้เหลือน้อยที่สุดเท่าที่จะเป็นไปได้
การใช้ตัวเก็บประจุแบบดีคัปปลิงเป็นวิธีที่มีประสิทธิภาพในการยับยั้งอิมพีแดนซ์ในระบบไฟฟ้า บทความนี้วิเคราะห์สาเหตุของการยับยั้งอิมพีแดนซ์ในระบบไฟฟ้าด้วยตัวเก็บประจุแบบดีคัปปลิง และระบุวิธีการต่าง ๆ ในด้านการเลือกใช้ตัวเก็บประจุแบบดีคัปปลิง นอกจากนี้ ยังมุ่งเน้นการวิจัยเกี่ยวกับวิธีการกำหนดตำแหน่งของตัวเก็บประจุแบบดีคัปปลิงบนพื้นฐานของการวิเคราะห์ฮาร์มอนิก เพื่อเพิ่มประสิทธิภาพสูงสุดในการยับยั้งอิมพีแดนซ์ในระบบไฟฟ้า
การวิเคราะห์อิมพีแดนซ์
กำลังไฟและกราวด์สามารถถือได้ว่าเป็นตัวเก็บประจุแผ่นขนาดใหญ่ซึ่งค่าความจุจะถูกคำนวณตามสูตรC=kAr/d
ในสูตรนี้kคือ 0.2249 นิ้ว;Aหมายถึงบริเวณขนานระหว่างระนาบสองระนาบรหมายถึงค่าคงที่ไดอิเล็กทริกของตัวกลาง และสำหรับวัสดุบอร์ด FR4 ที่ใช้กันทั่วไปมีค่าเท่ากับ 4.5ดหมายถึงระยะห่างระหว่างเพาเวอร์กับกราวด์ ตัวอย่างเช่น เลือกใช้แผ่น PCB ขนาด 2x1 นิ้ว ค่าความจุไฟฟ้าของตัวเก็บประจุที่เกิดจากเพาเวอร์และกราวด์ซึ่งมีพื้นที่ขนานกัน 20 มิล ประมาณเท่ากับ 0.2249x4.5x2x1/0.02=101.2pF จากสูตรนี้สามารถชี้ให้เห็นได้ว่า ค่าความจุสำหรับการดีคัปปลิงในระบบจ่ายไฟนั้นมีขนาดเล็กมาก ทำให้ค่าความต้านทานเชิงซ้อน (อิมพีแดนซ์) ที่สอดคล้องกันมีค่ามาก โดยทั่วไปอยู่ที่ระดับโอห์มหลายโอห์ม ดังนั้น การลดอิมพีแดนซ์ด้วยการดีคัปปลิงตัวเองภายในระบบจ่ายไฟเพียงอย่างเดียวจึงไม่เพียงพอ
มีการใช้เครื่องมือจำลอง SIWAVE ในระดับ 2.5D เพื่อดำเนินการจำลองอิมพีแดนซ์บนอุปกรณ์แอคทีฟ โดยเลือกเครือข่ายเพาเวอร์และกราวด์ U41 มาคำนวณพารามิเตอร์ XYZ ด้วยช่วงการสวีปตั้งแต่ 0 ถึง 1GHz ซึ่งได้เส้นโค้งอิมพีแดนซ์ดังแสดงในรูปที่ 1 ด้านล่าง
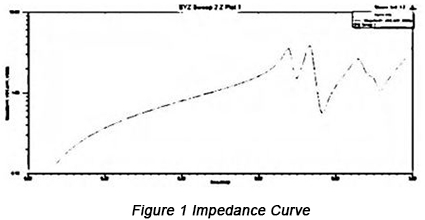
จากแผนภาพจะเห็นได้ว่าเส้นโค้งอิมพีแดนซ์มีการเปลี่ยนแปลงตามความถี่ที่เปลี่ยนไป และอิมพีแดนซ์มีการเปลี่ยนแปลงอย่างมากที่จุดเปลี่ยนซึ่งมีค่าอยู่ที่ 670MHz, 730MHz และ 870MHz
วิธีการห้าม
• การวิเคราะห์เชิงทฤษฎีเกี่ยวกับการห้ามอิมพีแดนซ์โดยใช้ตัวเก็บประจุแบบดีคัปปลิง
เนื่องจากไม่สามารถลดอิมพีแดนซ์ได้ด้วยการดีคัปปลิงจากแหล่งจ่ายไฟเอง จึงจำเป็นต้องใช้ตัวเก็บประจุดีคัปปลิงเพื่อยับยั้งอิมพีแดนซ์
รูปที่ 2 เป็นแผนผังของระบบกำลังแบบผสม รูปที่ 3 แสดงระบบกำลังนี้ในแบบจำลองกำลังสมมูล
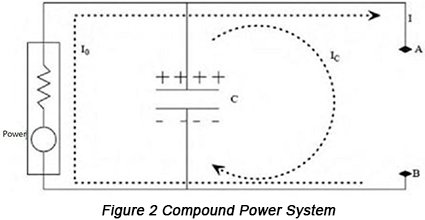
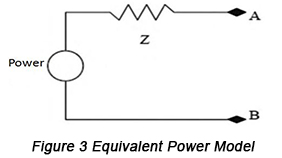
สามารถใช้สูตรเพื่อแทนวงจรนี้ได้:V=Zxแควรทำให้เกิดสภาวะที่ว่า แม้ว่ากระแสทรานเชียนต์ของโหลดจะยังคงมีการเปลี่ยนแปลงขนาดใหญ่ระหว่างจุด A และจุด B การเปลี่ยนแปลงของแรงดันไฟฟ้าระหว่างสองจุดนี้จะต้องมีขนาดเล็กมาก จากสมการนี้ เป้าหมายดังกล่าวไม่อาจบรรลุได้เลย เว้นแต่ว่าค่าของอิมพีแดนซ์ (Z) มีขนาดเล็กเพียงพอ ในรูปที่ 3 การใช้ตัวเก็บประจุแบบแยกส่วน (decoupling capacitor) มีประโยชน์ต่อการทำให้บรรลุเป้าหมายนี้ ดังนั้นจึงสามารถระบุได้ว่าตัวเก็บประจุแบบแยกส่วนมีความสามารถในการลดอิมพีแดนซ์ในระบบไฟฟ้าจากมุมมองของความสมมูล นอกจากนี้ จากมุมมองของหลักการวงจร ก็สามารถคงข้อสรุปเดียวกันได้ ตัวเก็บประจุมีลักษณะอิมพีแดนซ์ต่ำต่อสัญญาณกระแสสลับ ดังนั้น การมีส่วนร่วมของตัวเก็บประจุจึงทำให้มั่นใจได้ว่าจะช่วยลดอิมพีแดนซ์กระแสสลับในระบบไฟฟ้า
• การเลือกค่าความจุของตัวเก็บประจุสำหรับการแยกสัญญาณ
ไม่มีตัวเก็บประจุใดที่เป็นอุดมคติอย่างแท้จริง เนื่องจากจะมีพารามิเตอร์寄生อยู่เสมอ อิทธิพลที่ส่งผลต่อประสิทธิภาพความถี่สูงของตัวเก็บประจุมากที่สุดมาจาก ESR (ความต้านทานอนุกรมเทียบเท่า) และ ESL (ความเหนี่ยวนำอนุกรมเทียบเท่า) รูปที่ 4 แสดงแบบจำลองสมมูลที่คำนึงถึงพารามิเตอร์寄生เหล่านี้
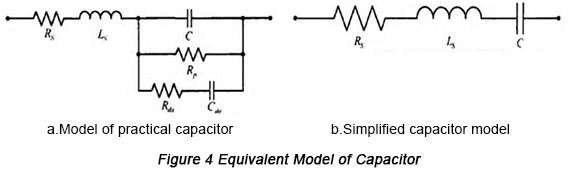
ตัวเก็บประจุยังสามารถถือได้ว่าเป็นวงจรฮาร์มอนิกแบบอนุกรม โดยที่ความถี่ฮาร์มอนิกแบบอนุกรมเป็นไปตามสมการ:f=1/2PIFC เมื่อมันอยู่ในสภาวะความถี่ต่ำ มันจะแสดงคุณสมบัติความจุ แต่เมื่อความถี่เพิ่มขึ้น มันจะแสดงคุณสมบัติความเหนี่ยวนำอย่างต่อเนื่อง กล่าวอีกนัยหนึ่ง อิมพีแดนซ์ของมันจะเพิ่มขึ้นก่อนแล้วจึงลดลงเมื่อความถี่สูงขึ้น และค่าต่ำสุดของอิมพีแดนซ์เทียบเท่าจะเกิดขึ้นที่ความถี่ฮาร์มอนิกแบบอนุกรมฟ0ในขณะนี้ รีแอกแตนซ์เชิงเก็บประจุและรีแอกแตนซ์เชิงเหนี่ยวนำหักล้างกันอย่างพอดี แสดงให้เห็นถึงความเท่ากันระหว่างค่าของอิมพีแดนซ์และ ESR โดยมีค่าความต้านทานเทียบเท่าของตัวเก็บประจุที่น้อยที่สุด เส้นโค้งความถี่ของตัวเก็บประจุแสดงไว้ในรูปที่ 5
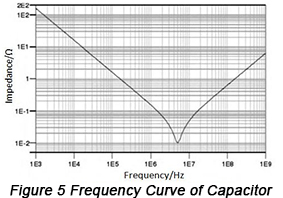
ดังนั้น ในกระบวนการเลือกตัวเก็บประจุ จุดความถี่ฮาร์มอนิกของตัวเก็บประจุที่เลือกจะอยู่ใกล้กับจุดความถี่ที่ต้องการการดีคัปปลิง สมรรถนะเชิงความจุของมันจึงต้องถูกนำมาใช้และใช้งานอย่างเต็มที่ให้มากที่สุดเท่าที่จะเป็นไปได้ ก่อนที่จะถึงจุดความถี่เรโซแนนซ์ตัวเอง
ตัวเก็บประจุที่มีค่าความจุไฟฟ้าแตกต่างกันและความถี่ฮาร์มอนิกตัวเองที่รองรับได้แตกต่างกันจะแสดงไว้ในตารางด้านล่าง
|
ความจุไฟฟ้า
|
DIP (MHz)
|
STM (MHz)
|
| 1.0μF |
2.5 |
5 |
| 0.1μF |
8 |
16 |
| 0.01μF |
25 |
50 |
| 1000pF |
80 |
160 |
| 100pF |
๒๕๐ |
500 |
| 10pF |
800 |
1.6(กิกะเฮิรตซ์) |
โดยทั่วไป จำเป็นต้องใช้คุณสมบัติฮาร์มอนิกของตัวเก็บประจุแบบดีคัปปลิง และสามารถได้มาซึ่งอิมพีแดนซ์ขาเข้าที่ต่ำที่สุดผ่านการต่อขนานของตัวเก็บประจุ การตอบสนองความถี่แบบขนานของตัวเก็บประจุชนิดเดียวกันจะแสดงไว้ในรูปที่ 6 ด้านล่าง
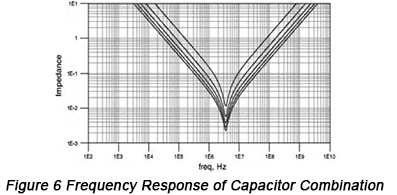
จากวิธีการนี้ สามารถลดค่า ESR และ ESL ที่เทียบเท่ากันได้อย่างมาก สำหรับตัวเก็บประจุหลายตัว (น) ที่มีค่าความจุไฟฟ้าเท่ากัน ค่าความจุไฟฟ้าสมมูล C จะกลายเป็น nC หลังจากการต่อรวมกัน ในขณะที่ค่าความเหนี่ยวนำสมมูลLกลายเป็นแ/นอย่างไรก็ตาม ค่า ESR ที่เทียบเท่าจะกลายเป็น R/n แต่ความถี่ฮาร์มอนิกยังคงไม่เปลี่ยนแปลง จะเห็นได้ว่าเนื่องจากความถี่ฮาร์มอนิกตัวเองมีค่าเท่ากันสำหรับตัวเก็บประจุชนิดต่าง ๆ ยิ่งต่อตัวเก็บประจุแบบขนานมากเท่าใด อิมพีแดนซ์ในบริเวณเชิงเก็บประจุและเชิงเหนี่ยวนำก็จะยิ่งน้อยลงเท่านั้น โดยที่จุดความถี่ฮาร์มอนิกตัวเองยังคงไม่เปลี่ยนแปลง
โดยสรุปแล้ว ในกระบวนการเลือกตัวเก็บประจุสำหรับการดีคัปปลิง ควรกำหนดความถี่ดีคัปปลิงให้เป็นจุดความถี่เรโซแนนซ์ตัวเองของการดีคัปปลิง เพื่อให้สามารถเลือกตัวเก็บประจุที่เหมาะสมได้ นอกจากนี้ การต่อขนานตัวเก็บประจุหลายตัวที่มีค่าความจุเท่ากันยังสามารถเพิ่มความสามารถในการดีคัปปลิงและลดอิมพีแดนซ์ได้
• การกำหนดตำแหน่งของตัวเก็บประจุแบบดีคัปปลิง
หลังจากเลือกตัวเก็บประจุสำหรับการดีคัปปลิงแล้ว จะต้องคำนึงถึงตำแหน่งของตัวเก็บประจุเหล่านั้นด้วย ระนาบจ่ายไฟและระนาบกราวด์สามารถมองได้ว่าเป็นโครงข่ายที่ประกอบด้วยตัวเหนี่ยวนำและตัวเก็บประจุหลายตัว หรือเป็นโพรงเรโซแนนซ์ ที่ความถี่หนึ่งๆ จะเกิดเรโซแนนซ์กับตัวเหนี่ยวนำและตัวเก็บประจุ ซึ่งมีผลต่ออิมพีแดนซ์ในระบบจ่ายไฟ เมื่อความถี่เพิ่มขึ้น อิมพีแดนซ์จะเปลี่ยนแปลงตลอดเวลา โดยเฉพาะเมื่อเรโซแนนซ์แบบขนานยังคงเด่นชัด อิมพีแดนซ์ก็จะเพิ่มขึ้นอย่างมากเช่นกัน ดังนั้น ตำแหน่งที่แน่นอนของตัวเก็บประจุสำหรับการดีคัปปลิงจึงควรกำหนดให้สอดคล้องกับการวิเคราะห์ฮาร์มอนิกของแผงวงจรพิมพ์ (PCB)
ด้วยการใช้ฟังก์ชันวิเคราะห์เรโซแนนซ์ของเครื่องมือจำลอง SIWAVE จะได้พารามิเตอร์สมมูล ได้แก่ ค่าความต้านทาน ค่าความจุ และค่าความเหนี่ยวนำ นอกจากนี้ ควรดำเนินการวิเคราะห์เรโซแนนซ์ของ PCB โดยใช้โหมดเรโซแนนซ์ที่ได้มาที่จุดความถี่ต่าง ๆ ดังแสดงในรูปที่ 7

เมื่อพิจารณาร่วมกับรูปที่ 1 จะสังเกตได้ว่าจุดความถี่หลายจุดที่มีอิมพีแดนซ์ค่อนข้างสูงนั้นสอดคล้องกับจุดความถี่ที่เกิดเรโซแนนซ์ ดังนั้น จากผลการวิเคราะห์เรโซแนนซ์จึงสามารถสรุปได้ว่า ในบริเวณที่เกิดเรโซแนนซ์รุนแรงควรติดตั้งตัวเก็บประจุแบบดีคัปปลิงที่มีค่าความจุเหมาะสมเพื่อช่วยลดอิมพีแดนซ์
ยกตัวอย่างจุดความถี่ที่ 673MHz สามารถวางตัวเก็บประจุแบบดีคัปปลิงแบบขนานกันได้เพื่อให้การเรโซแนนซ์หายไปและอิมพีแดนซ์ที่สอดคล้องกันถูกยับยั้ง ดังแสดงในรูปที่ 8

จากการวิเคราะห์เรโซแนนซ์ของแผ่นวงจรพิมพ์ (PCB) สามารถระบุตำแหน่งที่เกิดเรโซแนนซ์ได้ และจากข้อมูลดังกล่าวจึงทำการต่อคาปาซิเตอร์ขนาดที่เหมาะสมแบบขนานเข้าไปเพื่อยับยั้งอิมพีแดนซ์






















